2184 Number of Ways to Build Sturdy Brick Wall

🔀 Pick One

You are given integers height and width which specify the dimensions of a brick wall you are building. You are also given a 0-indexed array of unique integers bricks, where the ith brick has a height of 1 and a width of bricks[i]. You have an infinite supply of each type of brick and bricks may not be rotated.

Each row in the wall must be exactly width units long. For the wall to be sturdy, adjacent rows in the wall should not join bricks at the same location, except at the ends of the wall.

Return the number of ways to build a sturdy wall. Since the answer may be very large, return it modulo 109 + 7.

Example 1: 

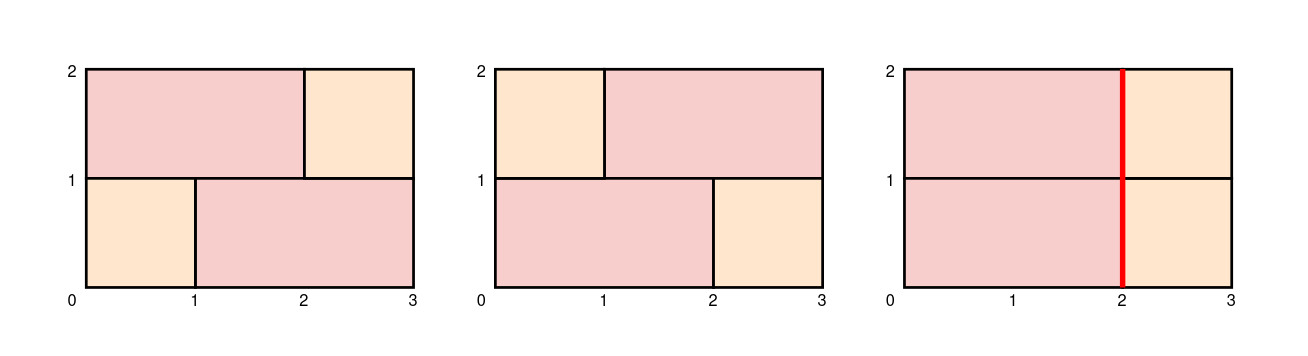
Input: height = 2, width = 3, bricks = [1,2]
Output: 2
Explanation:
The first two walls in the diagram show the only two ways to build a sturdy brick wall.
Note that the third wall in the diagram is not sturdy because adjacent rows join bricks 2 units from the left.

Example 2:

Input: height = 1, width = 1, bricks = [5]
Output: 0
Explanation:
There are no ways to build a sturdy wall because the only type of brick we have is longer than the width of the wall.

Constraints:

  • 1 <= height <= 100
  • 1 <= width <= 10
  • 1 <= bricks.length <= 10
  • 1 <= bricks[i] <= 10
  • All the values of bricks are unique.
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

class Solution:
    def buildWall(self, height: int, width: int, bricks: List[int]) -> int:
        # find all ways to build a line of bricks
        def dfs_comb(bricks_location: List[int], cur_length: int) -> None:
            if cur_length == width:
                combinations.append(bricks_location[:-1])
                return
            # go over all bricks
            for i, brick in enumerate(bricks):
                # check if exceed the length
                if cur_length + brick <= width:
                    # cur_length + brick is the next brick location
                    dfs_comb(bricks_location + [cur_length + brick], cur_length + brick)
                    
        # find ways to build a wall
        @cache
        def dfs_rows(row: int, h: int) -> int:
            if h == height:
                return 1
            cur = 0
            for i in adj[row]:
                cur += dfs_rows(i, h + 1)
            return cur
        
        combinations = []
        dfs_comb([],0)

        # find each line's possbile neighbors
        adj = defaultdict(list)
        for i, comb in enumerate(combinations):
            for j, neighbor in enumerate(combinations):
                # check if bricks at the same location
                if len(set(comb) & set(neighbor)) == 0:
                    adj[i].append(j)
        
        ans, mod = 0, int(1e9+7)
        for i in range(len(combinations)):
            ans += dfs_rows(i, 1) % mod
        return ans % mod