2021 Brightest Position on Street

A perfectly straight street is represented by a number line. The street has street lamp(s) on it and is represented by a 2D integer array lights. Each lights[i] = [positioni, rangei] indicates that there is a street lamp at position positioni that lights up the area from [positioni - rangei, positioni + rangei] (inclusive).

The brightness of a position p is defined as the number of street lamp that light up the position p.

Given lights, return the brightest position on the street. If there are multiple brightest positions, return the smallest one.

Example 1:

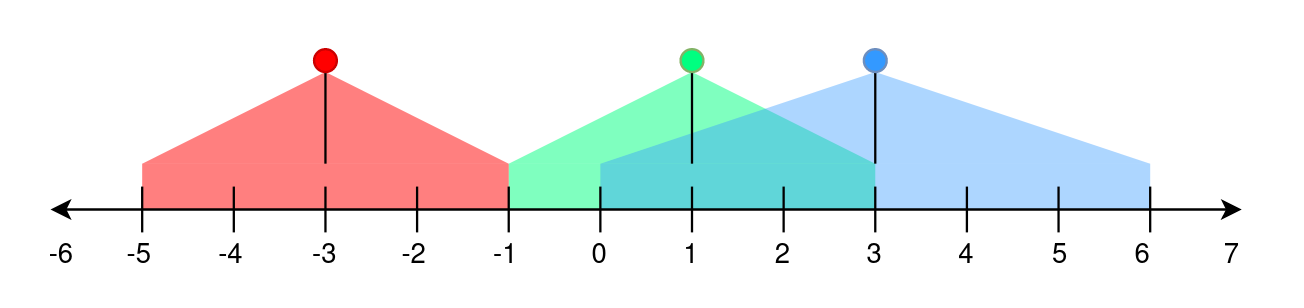
Input: lights = [[-3,2],[1,2],[3,3]]
Output: -1
Explanation:
The first street lamp lights up the area from [(-3) - 2, (-3) + 2] = [-5, -1].
The second street lamp lights up the area from [1 - 2, 1 + 2] = [-1, 3].
The third street lamp lights up the area from [3 - 3, 3 + 3] = [0, 6].

Position -1 has a brightness of 2, illuminated by the first and second street light.
Positions 0, 1, 2, and 3 have a brightness of 2,
illuminated by the second and third street light.
Out of all these positions, -1 is the smallest, so return it.

Example 2:

Input: lights = [[1,0],[0,1]]
Output: 1
Explanation:
The first street lamp lights up the area from [1 - 0, 1 + 0] = [1, 1].
The second street lamp lights up the area from [0 - 1, 0 + 1] = [-1, 1].

Position 1 has a brightness of 2, illuminated by the first and second street light.
Return 1 because it is the brightest position on the street.

Example 3:

Input: lights = [[1,2]]
Output: -1
Explanation:
The first street lamp lights up the area from [1 - 2, 1 + 2] = [-1, 3].

Positions -1, 0, 1, 2, and 3 have a brightness of 1,
illuminated by the first street light.
Out of all these positions, -1 is the smallest, so return it.

Constraints:

• 1 <= lights.length <= 105
• lights[i].length == 2
• -108 <= positioni <= 108
• 0 <= rangei <= 108

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution:
    def brightestPosition(self, lights: List[List[int]]) -> int:
        d = defaultdict(int)
        for light in lights:
            d[light[0] - light[1]] += 1
            d[light[0] + light[1] + 1] -= 1
        max_idx, max_val = -1, -1
        cur = 0
        for k in sorted(d.keys()):
            cur += d[k]
            if cur > max_val:
                max_idx = k
                max_val = cur
        return max_idx